
Nonlinear dynamical networks research published in Nature Communications

Above: Prof. Ying-Cheng Lai with Hongya Xu (center) and Guanglei Wang, both doctoral students in the School of Electrical, Computer and Energy Engineering. Photographer: Mihir Bhatt/ASU.
Electrical engineering Professor Ying-Cheng Lai, with his students and collaborators, has published a paper, A geometrical approach to control and controllability of nonlinear dynamical networks, in the prestigious Nature Communications, an open access journal that specializes in high-quality research from all areas of the natural sciences. One of the co-authors is Assistant Professor of biomedical engineering Xiao Wang.
According to Lai, the significance of the research is that in recent years, the focus of controlling complex networks has centered on controllability of networks hosting linear dynamics, leaving the more challenging problem of controlling nonlinear dynamical networks unaddressed. The paper examines the concept of attractor networks which, for the first time, allows the formulation of a quantifiable controllability framework for nonlinear dynamical networks. In particular, a network is more controllable if the underlying attractor network is strongly connected. The control framework was tested using examples from various models of experimental gene regulatory networks (GRNs). A counterintuitive finding is that due to nonlinearity, a proper amount of noise, or electromagnetic energy, can facilitate control, which was explained theoretically and demonstrated using GRNs.
“These findings are applicable to many kinds of complex infrastructures,” explains Lai. “For instance, the same principles can be applied to the power grids or to the energy flow in a modern, sophisticated building.”
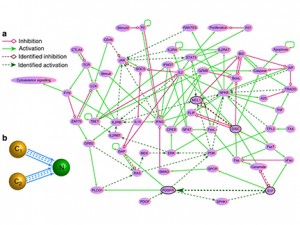
T-cell survival signalling network and its attractor network. Art courtesy of Ying-Cheng Lai.
Lai started collaborating with Wang, an expert in systems and synthetic biology, almost immediately after Wang joined the faculty at School of Biological and Health Systems Engineering. “I realized we could collaborate on a variety of problems in the interdisciplinary field of nonlinear dynamics, complex systems, systems and synthetic biology,” Lai says.
In biology, nonlinear dynamical networks with multiple attractors have been employed to understand fundamental phenomena such as cancer emergence, cell fate differentiation and cell cycle control. The study used GRNs to demonstrate the practicality of the control framework, which used low-dimensional, experimentally realizable synthetic gene circuits and a realistic T-cell cancer network of 60 nodes.
The research articulates control strategies and develops a controllability framework for nonlinear networks that exhibit multi-stability. A defining characteristic of such systems is that there are multiple coexisting attractors in the phase space. The goal is to drive the system from one attractor to another using physically realizable, temporary and finite parameter perturbation, assuming that the system is likely to evolve into an undesired state (attractor) or is already in such a state and, one wishes to implement control to bring the system out of the undesired state and steer it into a desired one.
The basic idea of attractor networks originated in Lai’s group through a long stretch of efforts, and was first discussed in a brief, perspective paper in the journal National Science Review. But according to Lai, placement in Nature Communications will bring more attention to the findings.


































